Present Value (PV): Understanding, Calculating, and Applications

Present Value emerges as a financial compass, guiding us through the intricacies of fiscal foresight. (PV), often likened to a crystal ball of finance, allows us to peer into the future and discern the true worth of monetary outcomes in the currency of today. As we embark on this exploration, we delve into the essence of Present Value—uncovering its significance, demystifying its calculations, and unveiling its indispensable role in shaping the financial landscape.

What is Present Value?

Present value, also known as discounted value, refers to the current worth of money that is expected to be received in the future. The concept of present value is rooted in the understanding that the value of money diminishes over time.

To illustrate the diminishing value of money over time, consider the example that one million tomans today would grant an individual greater purchasing power than the same amount in the next year. Conversely, a prudent investment has the potential to safeguard against the depreciation of currency.

Insights from Financial Managers on Present Value

While the idea might seem intricate, it boils down to a simple principle: $5,000 received today holds more value than $5,000 received five years from now. This is because, by opting for immediate receipt, one can invest the money and accrue additional returns over the ensuing five years.

The significance of calculating present value, or discounted value, is paramount in various financial computations. Notable examples include net (PV), bond yields, spot rates, and pension obligations, all of which hinge on the present value or discount principle. Proficiency in using financial tools such as calculators or software like Excel for (PV) calculations is invaluable. It aids in making informed decisions regarding financing options for significant purchases like a car or home and evaluating potential investments in new projects.

Present Value Formula and Calculation

Understanding the Present Value (PV) formula and its calculation is paramount in financial analysis, guiding decisions on investments, loans, and various financial transactions. The Present Value formula is expressed as:

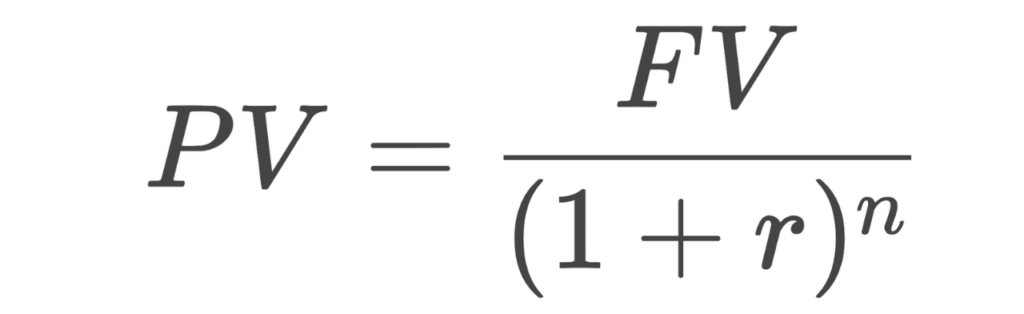
​Where:

• PV is the Present Value
• FV is the Future Value
• r is the discount rate
• n is the number of periods.

This formula reflects the principle that the value of money diminishes over time, and future cash flows are discounted to reflect their current worth. Let’s delve into the components of the formula:

1. Future Value (FV): This represents the amount of money expected to be received or paid in the future.
2. Discount Rate (r): Also known as the discount or interest rate, this factor reflects the rate at which future cash flows are adjusted to their present value. It considers the opportunity cost of tying up capital.
3. Number of Periods (n): This denotes the duration over which the future cash flow is expected. It could be in years, months, or any other relevant time unit.

By applying the present value formula, one can ascertain the current worth of a future sum of money, providing a basis for decision-making in financial matters. It is crucial in various financial calculations, including net present value (NPV), bond pricing, and determining the fair value of investments.

Calculation Present Value Example:

Consider an investment that promises $10,000 in two years with a discount rate of 5%. Applying the present value formula:

PV=10,000​\(1+0.05)^2

PV≈9,070.34

The present value of the $10,000 future cash flow, discounted at 5% for two years, is approximately $9,070.34. This means that, in present terms, the future $10,000 is equivalent to $9,070.34.

Mastering the present value formula empowers individuals and businesses to make informed financial decisions by evaluating the true worth of future cash flows in today’s terms.

Applications and Importance of Present Value

he concept of Present Value (PV) holds significant applications and importance across various financial scenarios. Here are some key applications and reasons for its importance:

Investment Valuation:

• Application: (PV) is widely used to assess the current worth of future cash flows from investments. It helps investors make informed decisions by comparing the (PV) of potential returns against the initial investment.
• Importance: It enables investors to evaluate the profitability of investments, considering the time value of money. This is crucial for making sound investment decisions in diverse financial markets.

Capital Budgeting:

• Application: (PV) is instrumental in capital budgeting decisions. It aids in evaluating the feasibility of long-term projects by discounting future cash flows to determine their (PV).
• Importance: This application ensures that companies allocate resources efficiently, considering the opportunity cost of tying up capital in long-term projects.

Loan and Mortgage Valuation:

• Application: Lenders use (PV) to assess the current value of future loan repayments or mortgage payments. Borrowers also use it to understand the real cost of borrowing.
• Importance: It helps both lenders and borrowers in making informed decisions about loans, ensuring transparency in understanding the true value of financial transactions.

Pension Fund Management:

• Application: (PV) is employed in determining the current value of future pension payments. Pension fund managers use it to ensure there are sufficient funds to meet future obligations.
• Importance: It plays a crucial role in pension fund management, helping maintain the financial health of retirement plans by accurately assessing future liabilities.

Business Valuation:

• Application: Business valuation often involves estimating the (PV) of expected future cash flows to determine the fair market value of a business.
• Importance: It provides a comprehensive and standardized method for assessing the intrinsic value of a business, aiding in strategic decision-making and financial planning.

Risk Assessment:

• Application: (PV) is utilized in assessing the risk associated with future cash flows. It helps quantify the impact of uncertainties on the current value of investments.
• Importance: This application assists in risk management, allowing individuals and organizations to make more informed decisions by considering the potential variability in future outcomes.

Time Management in Economics:

• Application: (PV) is a fundamental concept in time management within economics. It provides a suitable method for measuring the value of money in various economic situations.
• Importance: Understanding the time value of money is essential for individuals and businesses to navigate economic scenarios, ensuring financial decisions align with long-term goals.

In summary, the applications and importance of (PV) extend across diverse financial, investment, and economic contexts. Its versatility makes it a crucial tool for making sound financial decisions in both personal and business settings.

Advantages of Present Value

Informed Decision-Making:

Present value analysis empowers individuals and businesses to make informed decisions by providing a realistic evaluation of the current worth of future cash flows. This strategic approach is an advantage in navigating complex financial landscapes.

Time Value of Money Recognition:

By recognizing the time value of money, present value calculations highlight the distinctiveness that a sum of money today is inherently more valuable than the same amount in the future. This strategic insight guides individuals in prioritizing immediate gains and considering the opportunity cost of delayed receipts.

Risk Mitigation:

Present value offers a distinctive advantage in risk mitigation by allowing for a thorough assessment of the impact of uncertain future cash flows. The strategic discounting of these cash flows to their present value enables individuals to better evaluate and manage the potential risks associated with investments or financial commitments.

Disadvantages of Present Value

a. Opportunity Cost Consideration:

The determination of the discount rate involves evaluating the opportunity cost of capital, showcasing the distinctiveness of present value calculations. This strategic consideration ensures a fair and accurate representation of the time value of money.

b. Risk Assessment:

The discount rate’s dependence on risk assessment adds a distinctive layer to present value calculations. Higher-risk endeavors warrant a higher discount rate, strategically compensating for uncertainty. This nuanced approach enhances decision-making by acknowledging and addressing the distinctive risk profiles associated with different investments.

c. Adjusting for Inflation:

The distinctive advantage of present value lies in its strategic adjustment for inflation. Recognizing and accounting for inflation ensures that future cash flows are appropriately adjusted to their present value, guarding against underestimating the true cost or value of financial outcomes.

Limitations of Present Value

a. Assumption Sensitivity:

Despite its advantages, (PV) calculations are sensitive to assumptions. Small variations in assumptions can lead to significant differences, emphasizing the need for a strategic understanding of the inherent sensitivity in decision-making.

b. Difficulty in Future Cash Flow Estimation:

The distinctive challenge of precise future cash flow estimation is a limitation that needs to be strategically addressed. Recognizing the strategic importance of accurate estimations, despite inherent challenges, is crucial for a well-informed decision-making process.

c. Neglects Non-Monetary Factors:

While presenting distinctive advantages in monetary assessments, (PV) calculations may neglect non-monetary factors. A strategic approach involves supplementing the analysis with a broader perspective that considers the distinctiveness of qualitative elements in decision-making.

Additional Insights on (PV)

Time Horizon Considerations:

• (PV) is particularly useful when comparing projects or investments with different time horizons. It allows for a standardized assessment by bringing all cash flows to their (PV), providing a fair basis for comparison.

Real vs. Nominal Cash Flows:

• (PV) is sensitive to the choice between real (adjusted for inflation) and nominal (actual) cash flows. Understanding when to use real or nominal cash flows in calculations is crucial for accurate valuation.

Discount Rate Variations:

• Exploring the impact of varying discount rates on (PV) can offer valuable insights. Sensitivity analysis, where the discount rate is adjusted to observe its influence on (PV), helps in assessing the robustness of financial decisions.

Application in Diverse Financial Instruments:

• (PV) is not limited to investment decisions. It is also widely used in valuing bonds, assessing lease agreements, and determining the fair value of various financial instruments. Exploring these applications adds depth to the understanding of (PV).

Relationship with Net Present Value (NPV):

• Introduce the concept of Net (PV), which is derived from (PV). NPV considers both inflows and outflows, providing a comprehensive assessment of the profitability of an investment. Understanding NPV complements the insights gained from (PV) calculations.

Challenges in Cash Flow Patterns:

• Consider discussing scenarios where cash flows are irregular or non-uniform. (PV) is versatile enough to handle uneven cash flow patterns, and understanding how to adapt calculations in such situations is beneficial.

Global Economic Factors:

• Acknowledge the influence of global economic factors on discount rates. Changes in interest rates, inflation rates, and geopolitical events can significantly impact the discount rate, affecting the outcomes of (PV) analyses.

Ethical Considerations:

• (PV) calculations play a role in ethical decision-making. Understanding the financial implications of decisions, especially in situations involving long-term commitments, adds an ethical dimension to the use of (PV).

Conclusion

As we conclude our journey through the intricacies of Present Value, we emerge with a newfound appreciation for its prowess. Beyond a mere financial tool, (PV) stands as a sentinel, guiding us through the complexities of decision-making with a keen eye on the future. From adjusting for inflation to assessing risk and exploring diverse financial instruments, Present Value is the linchpin that connects financial wisdom with actionable insights.

In an ever-evolving financial landscape, the principles of (PV) remain a steadfast ally, offering clarity in uncertainty and strategic foresight in every financial endeavor. As we navigate the financial horizon, may the lessons learned here echo in your financial decisions, contributing to a future built on the foundation of present-day wisdom.

Stay financially savvy, stay empowered.

FAQ